Factorización de un trinomio
Un trinomio es una expresión algebraica que consta de tres términos.
Algunos trinomios se pueden expresar como el producto de sus factores (factorizado) y cuando esto es posible se facilita el trabajo de determinar los ceros del polinomio. Además, es de práctica común modelar operaciones algebraicas mediante el empleo de la geometría, en cuyo caso factorizar la expresión es el camino más fácil para determinar las dimensiones de la figura, siempre que sea posible.
Trinomios de la forma \(ax^{2n}+bx^n+c\)
Son trinomios de la forma \(ax^{2n}+bx^n+c\) todos aquellos trinomios en los cuales el exponente del primer término es el duplo del exponente del segundo término y \(c\) es un número cualquiera. Algunos ejemplos de estos trinomios son
$$ax^{2n}+bx^n+c\Longrightarrow\left\{\begin{array}0\frac{1}{2}{at}^2+v_0t+d_0\ \\ 3u^4+2u^2+6\\h^{10}+5h^5+4\\x^\frac{2}{5}+5x^\frac{1}{5}+4\end{array}\right.$$
Como ya se ha dicho algunos trinomios \(ax^{2n}+bx^n+c\) se pueden factorizar y de estos, los más estudiados son los trinomios cuadrados perfectos (t.c.p.), los de la forma \(x^2+bx+c\) y de la forma \(ax^2+bx+c\).
Se pueden ver las factorización de estos trinomios haciendo clic en la pestañas de arriba.
Trinomios de la forma \(x^2+bx+c\)
Si \(a\) y \(n\) son iguales a uno en el trinomio \(ax^{2n}+bx^n+c\) este se transforma en \(x^2+bx+c\) y el procedimiento para su factorización si no existe un m.c.d. es como sigue.
Factorización del trinomio de la forma \(x^2+bx+c\)
1. En \(x^2+bx+c\) extraer la raíz del primer término \(\Longrightarrow\sqrt{x^2}=x\).
2. Se forma dos factores con esta raíz en la forma:
\((x~{\rm signo~de~} b~ \textcolor{#ff0080}{h})(x~{\rm~signo~del~producto~} bc~ \textcolor{#ff0080}{k})\) de donde resulta una de esta forma:
\((x+h)(x+k)\), \((x+h)(x-k)\), \((x-h)(x+k)\) ó \((x-h)(x-k)\)
donde \(h>k\) si los signos son distintos.
3. Escribir los números \(h\) y \(k\) que cumplen con las condiciones siguientes:
3.1 \(hk=c\) y \(h+k=b\) si \(h\) y \(k\) son de signos iguales.
3.2 \(hk=c\) y \(h-k=b\) si \(h\) y \(k\) son de signos distintos.
Ejemplo factorizar \(x^2+14x+13\)
Solución: El trinomio es de la forma \(x^2+bx+c=(x+h)(x+k)\) donde \(hk=13\) y \(h+k=14\), por los que \(h=13\) y \(k=1\) de donde se tiene \(x^2+14x+13=(x+13)(x+1)\)
Ejemplo factorizar \(x^2-6x-55\)
Solución: El trinomio es de la forma \(x^2+bx+c=(x-h)(x+k)\) donde \(hk=55\) y \(h-k=6\), por los que \(h=13\) y \(k=1\) de donde \(x^2-6x+-55=(x-11)(x+5)\)
Ejemplo factorizar \(x^2+26x+169\)
Solución: El trinomio es de la forma \(x^2+bx+c=(x+h)(x+k)\) donde \(hk=169\) y \(h+k=26\), por los que \(h=13\) y \(k=13\) de donde \(x^2-6x+-55=(x+13)(x+13)=(x+13)^2\)
También puede factorizar el trinomio \(x^{2n}+bx^n+c=\left(x^n+h\right)\left(x^n+k\right)\) donde \(h\) y \(k\) cumplen las mismas condiciones del trinomio \(x^2+bx+c\) anteriores.
Ejemplo factorizar \(x^{10}+38x^5+357\).
Solución: el trinomio es de la forma \(x^{2n}+bx^n+c=\left(x^n+h\right)\left(x^n+k\right)\) por tanto, escriba \(x^{10}+38x^5+357=\left(x^5+h\right)\left(x^5+k\right)\) donde \(hk=357\) y \(h+k=38\) Para determinar los valores de \(h=18\) y \(k=14\) que cumplen las condiciones se descompone 357 en factores primos (realizar la “parrilla”), de donde se tiene \(h=21\) y \(k=17\) y se concluye que:
\(x^{10}+38x^5+357=\left(x^5+21\right)\left(x^5+17\right)\)
Ejemplo factorizar \(x^6+4x^3-252.\)
Solución: el trinomio es de la forma \(x^{2n}+bx^n+c=\left(x^n+h\right)\left(x^n+k\right)\) por tanto, escriba \(x^6+4x^3-252=\left(x^3+h\right)\left(x^3-k\right)\) donde \(hk=252\) y \(h-k=4\). Usando la descomposición prima (parrilla) para determinar los valores de \(h=18\) y \(k=14\) y se concluye que:
\(x^6+4x^3-252=\left(x^3+18\right)(x^3-14)\)
Trinomios de la forma \(ax^{2n}+bx^n+c\).
Si \(a\neq1\) en \(ax^{2n}+bx^n+c\) y \(n=1\) se tiene \(ax^2+bx+c\) y el procedimiento para su factorización si no existe un m.c.d. se puede realizar por multiplicación y división o mediante agrupación.
I. Factorización de \(ax^2+bx+c\) mediante multiplicación y división.
1. Multiplicar y dividir \(ax^2+bx+c\) por el coeficiente \(a\) dejando expresada la primera y segunda multiplicación, escribiendo en la forma: $$ax^2+bx+c=\frac{\left(ax\right)^2+b\left(ax\right)+m}{a}\ \ \ \ \ para\ m=ac$$ Esto es, porque solo necesita realizar la última multiplicación.
2. Factorizar el numerador de la expresión anterior como si fuera un trinomio \(x^2+bx+c\), esto es, $$\frac{\left(ax\right)^2+b\left(ax\right)+m}{a}=\frac{(ax~ {\rm signo~ de~b}~\textcolor{#ff0080}{h})(ax ~{\rm signo~de~bc}~\textcolor{#ff0080}{k})}{a}$$ donde \(\textcolor{#ff0080}{hk}=m\) y además \(h+k=b\) si los signos de los factores son iguales o \(h-k=b\) si los signos de los factores son distintos, para \(h>k\)
3. Simplificar el denominador de la expresión, factorizando un m.c.d. en el numerador, de donde queda, \(ax^2+bx+c=(dx+u)(wx+v)\)
II. Factorización del trinomio \(ax^2+bx+c\) por agrupación de términos.
1. Multiplicar \(ac\)
2. Determinar dos números \(h\) y \(k\) tales que:
2.1 \(hk=ac\) y \(h+k=b\) si el producto de los signos de \(b\) y \(c\) es el signo de \(b\).
2.2 \(hk=ac\) y \(h-k=b\) si el producto de los signos de \(b\) y \(c\) no es el signo de \(b\).
3. Escribir el trinomio \(ax^2+bx+c\) como \(ax^2+hx+kx+c\) y factorizar por agrupación.
El trinomio \(ax^{2n}+bx^n+c\) se factoriza como si fuera \(ax^2+bx+c\) ya sea por multiplicación y división, o por agrupación de términos.
Trinomio cuadrado perfecto t.c.p.
Un trinomio \(ax^{2n}+bx^n+c\) es cuadrado perfecto si y solo si cumple dos condiciones:
1. El primer y tercer término son positivos.
2. El segundo término, sin considerar el signo, es el duplo del producto de las raíces cuadradas del primer y tercer término.
Son trinomios cuadrados perfectos las expresiones:
1.\(x^2+14x+49\) 2.\(w^{10}-10w^5+25\) 3.\(x^2+2\sqrt3x+3\) 4.\(x^2+4\sqrt3x+12\) mientras que \(x^{10}-8x^5+49\) y \(w^4-2w^2-1\) no lo son.
\(x^{10}-8x^5+49\) no cumple la condición dos, \(8x^5\neq2\sqrt{x^{10}}\sqrt{49}=14x^5\) y para \(w^4-2w^2-1\) el tercer término es negativo.
Factorización de un trinomio cuadrado perfecto (t.c.p.)
Regla: Para factorizar un t.c.p. se determinan las raíces cuadradas del primer y tercer término, se separan por el signo del segundo término y se eleva esta suma o diferencia al cuadrado, esto es \((\sqrt{1^{er}~\mathrm{término}} ~~\mathrm{signo~~ del~ segundo}~~\sqrt{3^{er}~\mathrm{término}})^2\).
Ejemplo 1. Verificar si los siguientes trinomios son t.c.p. si lo son, factorizarlos.
1.\(u^2-20u+100\) 2.\(u^6+2\sqrt{13}u^3+13\) 3.\(u^4-6u^2-4\) 4.\(16x^{10}+24x^5+9\)
Análisis: si los trinomios son t.c.p. deben cumplir las condiciones: 1. Primer y tercer término positivos. 2. El segundo término es el duplo del producto de las raíces cuadradas del primer y tercer término. verificando esto se tiene:
1.1 Para \(u^2-20u+100\Longrightarrow\) primer y tercer términos son positivos y \(20u=2\sqrt{u^2}100\) por tanto, es un t.c.p. y se factoriza como \((u-10)^2\)
1.2 Para \(u^6+2\sqrt{13}u^3+13\Longrightarrow\) primer y tercer términos son positivos y \(2\sqrt{13}u^3=2\sqrt{u6}\sqrt{13}\) por tanto es un t.c.p. y se factoriza como \((u^3+\sqrt{13})^2\)
1.3 Para \(u^4-6u^2-4\) el tercer término es negativo, así que no es un t.c.p.
1.4 Para \(16x^{10}+24x^5+9\Longrightarrow\) primer y tercer término son positvos y \(2\sqrt{16x^{10}}\sqrt{9}=2(4x^5)3=24x^5\) por tanto es un t.c.p. y se factoriza como \((4x^5+3)^2\)
T.C.P. por adición y sustracción.
Algunas veces al intentar factorizar un trinomio, este no se ajusta a ninguna de las formas conocidas, en estos casos se puede factorizar por medio del artificio matemático de “sumar un cero” al trinomio, mediante la adicción y sustracción de una misma cantidad, para convertirlo en un t.c.p. y luego factorizar la expresión resultante, mediante agrupación de términos y diferencia de cuadrados.
Ejemplo. Factorizar el trinomio \(x^2+4x+16\)
Análisis: \(x^2+4x+16\) es de la forma \(x^2+bx+c\) por lo cual de manera natural se piensa en su factorización como \(\left(x+h\right)\left(x+k\right)\), el hecho es que no existen ningún par de números \(h\) y \(k\) los cuales cumplan la condiciones \(hk=16\) y \(h+k=4\), esto implica también que no es un t.c.p. ya que todos los t.c.p. son trinomios factorizables. Sin embargo, mediante el proceso de adición y sustracción se puede hacer que \(x^2+4x+16\) sea un t.c.p. y factorizar el trinomio como sigue:
Comience por notar que para que \(x^2+4x+16\) sea un t.c.p. el segundo término debe ser \(8x\) y no \(4x\), por tanto, sume y reste \(4x-4x=0\) para completar el t.c.p. y factorice como sigue.
\(x^2+4x+16\) Trinomio dado en el ejercicio.
\(x^2+4x+16+4x-4x\) Sumando \(4x-4x=0\) para tener el T.C.P.
\(\left(x^2+4x+4x+16\right)-4x\) Agrupando y ordenando términos.
\(\left(x^2+8x+16\right)-4x\) Simplificando
\(\left(x+4\right)^2-4x\) Factorizando el t.c.p.
\(\left(x+4-2\sqrt x\right)\left(x+4+2\sqrt x\right)\)Factorizando la diferencia de cuadrados.
\(\left(x-2\sqrt x+4\right)\left(x+2\sqrt x+4\right)\) Ordenando.
Ejemplo 2. Factorizar \(x^4-38x^2+1\)
Solución: \(x^4-38x^2+1\) es de la forma \(x^{2n}+bx^n+c\) por tanto su factorización es de la forma \(\left(x^2-h\right)\left(x^2-k\right)\), sin embargo, no existen dos números h y k tales que \(hk=1\) y además \(h+k=38\). Note que para \(x^4-38x^2+1\) ser un T.C.P. el segundo término debe ser \(-2x^2\) y no \(-38x^2\) por tanto, sume \(36x^2-36x^2=0\) para así completar el T.C.P. y factorizar.
\(x^4-38x^2+1\) Trinomio dado.
\(x^4-38x^2+1+36x^2-36x^2\) Sumando \(36x^2-36x^2=0\) para el t.c.p.
\(\left(x^4-38x^2+36x^2+1\right)-36x^2\) Agrupando y ordenando términos.
\(\left(x^4-2x^2+1\right)-36x^2\) Simplificando.
\(\left(x^2-1\right)^2-36x^2\) Factorizando el T.C.P.
\(\left(x^2-1+6x\right)\left(x^2-1-6x\right)\) Factorizando la diferencia de cuadrados.
\(\left(x^2+6x-1\right)\left(x^2-6x-1\right)\) Ordenando.
Ampliando saberes. Los t.c.p. son trinomios de la forma \(ax^{2n}+bx^n+c\). Además, algunos trinomios de la forma \(ax^{2n}+bx^n+c\) puede tener más de una variable, como las expresiones \(9x^2+6xy+y^2\) o \(100w^4x^2+50w^2xh+25h^2\) en ambos casos puede factorizar como desee.
Por último, al factorizar una expresión algebraica cualquiera, debe iniciar por contar los términos del polinomio para identificar el tipo de polinomio que es la expresión dada, así podrá tener una idea de la posible regla a usar. Además, siempre que en \(ax^{2n}+bx^n+c\) el coeficiente \(a\neq1\) conviene probar si el trinomio es t.c.p. como primera opción.
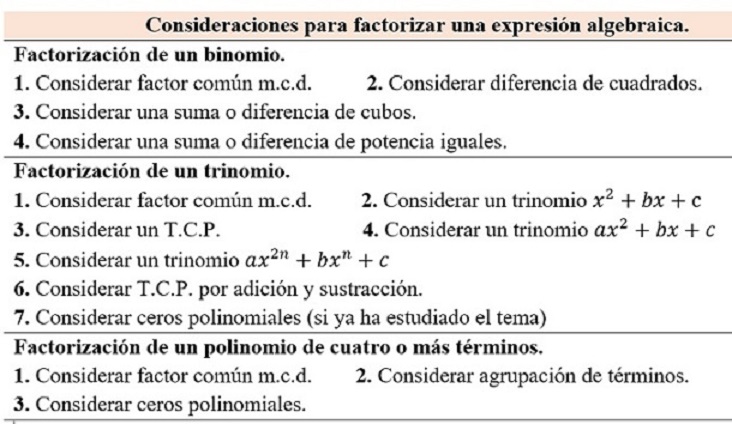
A continuación, se presenta en forma de tabla algunas consideraciones importantes que debe tener en cuenta al momento de factorizar.
Factorización y geometría. El área de un solar rectangular está dada por la expresión \(A=x^2+16x+48\). Determinar las longitudes de los lados y la medida de su contorno.
El área de un terreno rectangular está dada por la expresión \(A=3x^2-7x-6\). Determine el perímetro del terreno.
El área de un rectángulo está dada por la expresión \(A=6x^2-5x-21\). Determinar las longitudes de sus lados.
El área de un rectángulo está dada por la expresión \(A=u^2-20u+100\). Determinar si es o no un cuadrado.
Escribir \(P\left(x\right)=x^4-5x^2+4\) como el producto de factores lineales.
Como afecta un cambio de signo la factorización. Factorizar los trinomios:
\(1.~~ x^2+37x+36~~~\) \(2.~~ x^2-37x+36~~~\) \(3.~~ x^2+37x-36\)
Factorizar \(100w^4x^2+100w^2xh+25h^2\)
Factorizar \(7w^2x-60x^2+w^4\)
Factorizar los polinomios siguientes, \begin{align} &1.~~n^2-46n+448\\ &2.~~w^2-9w-1620\end{align}.
Factorizar los trinomios siguientes. \begin{align} &1.~~u^6+4u^3-252\\ &2.~~x^\frac{2}{5}+5x^\frac{1}{5}+4\\ &3.~~7w^2x-60x^2+w^4 \end{align}
Ej.11
